728x90
주성분 분석(PCA)
- 상관관계가 있는 고차원 자료를 자료의 변동을 최대한 보존하는 저차원 자료로 변환시키는 방법
- 자료의 차원을 축약시키는데 주로 사용
- p차원 변수에서 분산이 가장 큰 선형변환을 첫 번째 주성분이라고 하고, 그 다음 큰 선형변환이 두 번째 주성 분이라고 함
- 주성분들은 차원을 줄여 예측 모델을 만들 때도 사용
- 희생되는 정보가 가장 적은 방향을 결정
주성분 분석의 목적
- 소수의 주성분으로 차원을 축소
- 다중공선성이 존재하는 경우, 상관성이 없는 주성분으로 변수들을 축소 → 회귀분석이나 의사결정나무
- 군집분석시 군집화 결과와 연산속도를 개선
주성분 선택법
- 주성분 분석의 결과에서 누적기여율이 85% 이상이면 주성분의 수로 결정
- scree plot을 활용하여 고유값이 수평을 유지하기 전단계로 주성분의 수를 선택
예제)
# 주성적 분석 PCA
library(datasets)
data(USArrests)
pairs(USArrests, panel =panel.smooth) # Murder와 UrbanPop비율간의 관련성은 작음
US.prin <- princomp(USArrests, cor=TRUE) # princomp 함수로 주성분 분석(상관계수 행렬 사용한다.)
summary(US.prin) # 4개 주성분의 표준편차, 분산의 비율을 보여준다.
screeplot(US.prin,npcs=4, type="lines") # 주성분들에 의해 설명되는 변동의 비율을 확인한다.
loadings(US.prin) # 기여하는 가중치 제시
US.prin$scores #각 주성분의 선형식을 통해 각 지역별로 얻은 결과를 계산
arrests.pca <- prcomp(USArrests, center=TRUE, scale.=TRUE)
biplot(arrests.pca,scale=0) # 관측치를 첫 번째와 두 번째 주성분의 좌표 에 그린다.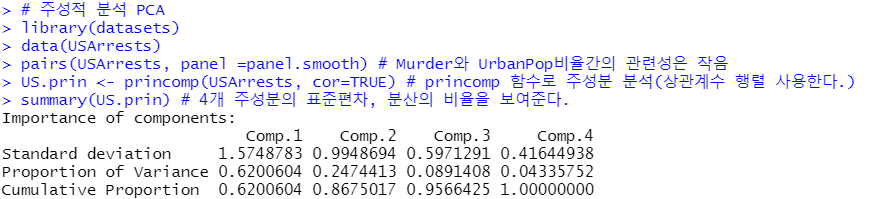





출처 : 2020 전면 개정판 ADsP 데이터 분석 준전문가 DATAEDU
728x90