728x90
시계열 모형
이동평균모형(Moving Average model , MA 모형)
- 이동평균 : 과거로부터 현재까지의 시계열 자료를 대상으로 일정기간별 이동평균을 계산하고, 이들의 추 세를 파악하여 다음 기간을 예측
- 이동평균모형은 유한개의 백색잡음의 선형 결합이므로 언제나 정상성을 만족
- 1차 이동평균모형, MA(1) 모형 : 가장 간단한 이동평균모형으로 같은 시점의 백색잡음과 바로 전 시점의 백색잡음의 결합으로 이루어진 모형
- 2차 이동평균모형, MA(2) 모형 : 바로 전 시점의 백색잡음과 시차가 2인 백색잡음의 결합으로 이뤄진 모형
- 자기상관함수 : p+1 시차 이후 급격히 감소하여 절단된 형태, MA(p) 모형
- 부분자기상관함수 : 점차 감소하는 형태
예) 전기사용량 : 봄보다 여름이 많아지고 가을에 다시 사용량이 적어진다. 이런 경우 이동평균모형을 이용한다.
자기회귀누적이동평균모형(ARIMA 모형)
- 대부분의 많은 시계열 자료가 자기회귀누적이동평균모형을 따름
- ARIMA 모형은 기본적으로 비정상 시계열 모형
- → 차분이나 변환을 통해 AR 모형이나 MA 모형, ARMA 모형으로 정상화할 수 있음
ARIMA 전에 ARMA모델이 존재 - ARMA : AR+MA
① ARIMA(p,d,q) 모형
- p,d,q의 값에 따라 모형의 이름이 다르게 됨
- 차수 p : AR 모형과 관련
- 차수 q : MA 모형과 관련,
- 차수 d : ARIMA에서 ARMA로 정상화할 때 몇 번 차분을 했는지를 의미
- d=0이면 → ARMA(p,q) 모형이라 부르고, 정상성을 만족.
- p=0이면 → IMA(d,q) 모형이라고 부르고, d번 차분 → MA(q)
- q=0이면 → ARI(p,d) 모형이며, d번 차분한 시계열 모형 → AR(p) 모형
예제)
# ARIMA 모형 예제
install.packages("tseries")
install.packages("forecast")
library(tseries) # 시계열 분석 위한 패키지
library(forecast) # 시계열 예측을 위한 패키지
king <- scan("http://robjhyndman.com/tsdldata/misc/kings.dat",skip=3) # 3라인을 건너뛰고 벡터로 저장
king.ts <- ts(king) # 시계열 데이터 생성
plot(king.ts)
king.ff1 <- diff(king.ts,differences=1) # 1차 차분
plot.ts(king.ff1)
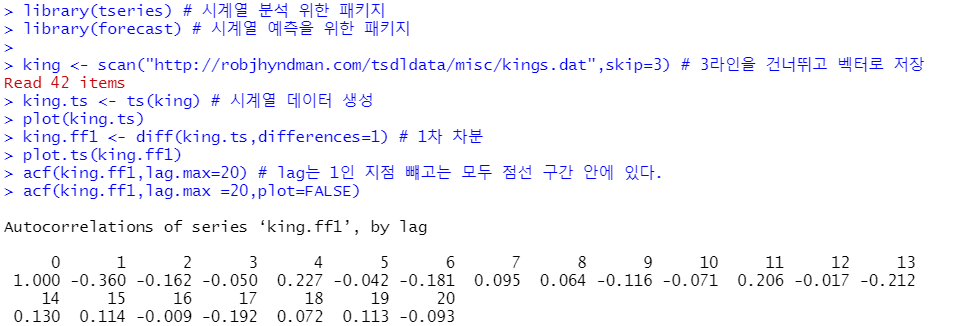
acf(king.ff1,lag.max=20) # lag는 1인 지점 뺴고는 모두 점선 구간 안에 있다.
acf(king.ff1,lag.max =20,plot=FALSE)
pacf(king.ff1,lag.max=20) # 1,2,3에서 점선 구간을 초과하고 음의 값을 가지며 절단점이 lag4
pacf(king.ff1,lag.max = 20, plot=FALSE)
auto.arima(king) # 적절한 아리마 모형을 찾아준다
king.arima <- arima(king,order=c(0,1,1)) # 선정된 아리마 모형으로 데이터를 보정한다.
king.forecast <- forecast(king.arima) # ARIMA 모형에 의해 보정된 데이터를 통해 미래값을 예측한다.
king.forecast








분해 시계열
- 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법
- 시계열 구성 요소
① 추세 요인(trend factor)
- 자료가 특정한 형태를 취할 때 추세 요인이 있다고 한다.(선형적, 이차식, 지수 형태)
② 계절 요인(seasonal factor)
- 고정된 주기에 따라 자료가 변화하는 경우(요일,월,사분기자료에서 분기 변화)
③ 순환 요인(cyclical factor)
- 명백한 경제적이나 자연적인 이유가 없이 알려지지 않은 주기를 가지고 변 화하는 자료
④ 불규칙 요인(irregular factor)
- 위의 3가지 요인으로 설명할 수 없는 회귀분석에서 오차에 해당하는 요인
예제)
# 시계열 자료를 추세요인, 계졀요인, 불규칙요인으로 분해
ldeaths.decompose <- decompose(ldeaths)
plot(ldeaths.decompose)

출처 : 2020 전면 개정판 ADsP 데이터 분석 준전문가 DATAEDU
728x90