728x90
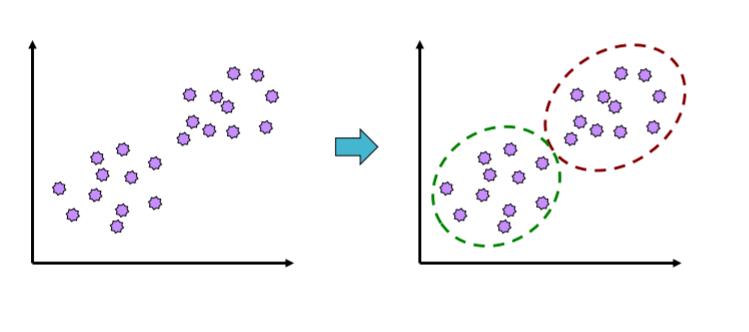
1. 군집 분석(cluster analysis)
- 각 개체에 대해 관측된 여러 개의 변수 값들로부터 n개의 개체를 유사한 성격을 가지는 몇 개의 군집으로 집단화하고, 형성된 군집들의 특성을 파악하여 군집들 사이의 관계를 분석하는 다변량 분석 기법
- 다변량 자료는 별도의 반응변수가 요구되지 않으며, 오로지 개체들 간의 유사성(similarity)에만 기초하여 군집을 형성
- 이상값 탐지, 심리학, 사회학, 경영학, 생물학 등에 이용
- 군집화의 방법 : 계층적 군집, 분리 군집, 밀도-기반 군집, 모형-기반 군집, 격자-기반 군집, 커널 -기반 군
- 집, SOM(Self-Organization Map)

2. 계층적 분석(hierarchical clustering)
- 가장 유사한 개체를 묶어 나가는 과정을 반복하여 원하는 개수의 군집을 형성하는 방법
- 덴드로그램(dendrogram) 형태로 결과가 주어짐
- 각 개체는 하나의 군집에만 속하게 됨
- 개체간의 유사성(또는 거리)에 대한 다양한 정의가 가능
- 작은 군집으로부터 출발하여 군집을 병합해 나가는 병합적 방법과 큰 군집으로부터 출발하여 군집을 분리해 나가는 분할적 방법이 있음
- 군집간의 거리 측정 방법 : 최단연결법, 최장연결법, 평균연결법, 중심연결법, 와드연결법
3. 거리 측정 방법
- ① 최단 연결법, 단일연결법(single linkage method) : 거리의 최소값으로 측정
- ② 최장 연결법, 완전연결법(complete linkage method) : 거리의 최대값으로 측정
- ③ 중심 연결법(centroid linkage) : 두 군집의 중심 간의 거리를 측정
- ④ 평균 연결법(average linkage) : 모든 항목에 대한 거리 평균을 구함
- ⑤ 와드 연결법(ward linkage) : 군집 내의 오차제곱합에 기초하여 군집을 수행

4. 거리
- 연속형 변수 : 유클리디안 거리, 표준화 거리, 마할라노비스 거리, 체비셰프 거리, 맨하탄 거리, 캔버라 거리, 민코우스키 거리
- 범주형 변수 : 자카드 거리, 자카드 계수, 코사인 거리, 코사인 유사도(벡터 내적의 코사인 값을 이용)
예제 ) USArrest 자료는 미국 50개 주에서 1973년에 발생한 폭행, 살인, 강간 범죄를 주민 100,000명 당 체포된 사람의 통계 자료다.
# 정형 데이터 마이닝
data(USArrests) # USArrests자료는 미국 50개 주 1973에 발생한 범죄 자료
str(USArrests)
d <- dist(USArrests, method ="euclidian")
fit <- hclust(d,method="ave")
par(mfrow=c(1,2))
plot(fit)
plot(fit,hang=-1)
par(mfrow=c(1,1))


728x90