이산확률분포

이산확률분포(Discrete Probability Distribution)

• 확률변수 $X$가 취할 수 있는 모든 값이 유한하거나 셀 수 있는 무한한 경우, 이를 이산확률변수라고 한다. 
• 이때 이산확률분포는 이산확률변수의 확률분포를 의미
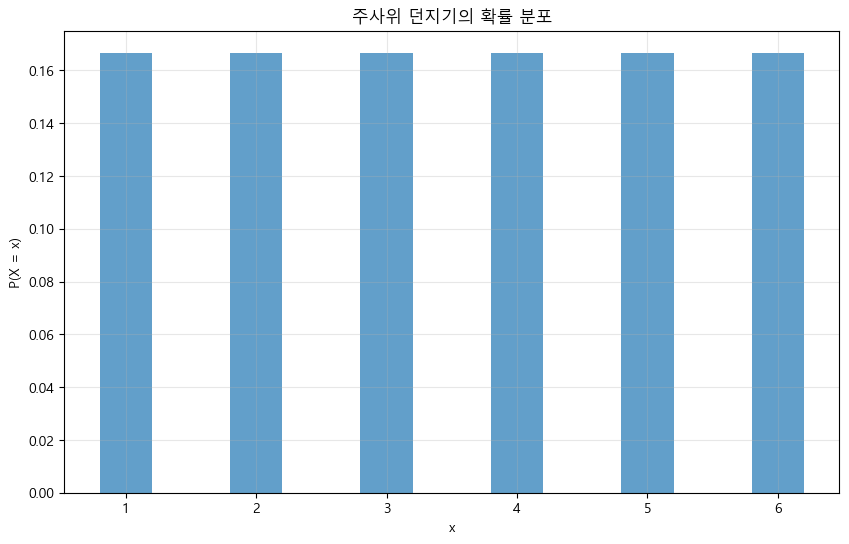
• 예시 : 주사위 던지기
  • 주사위를 던졌을 때 나올 수 있는 눈금(수)을 확률변수 $X$라고 하자.
  • 확률변수 $X$는 {1,2,3,4,5,6} 중 하나의 값을 가질 수 있다. 

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

def plot_discrete_distribution(x_values, probabilities, title):
    """이산확률분포를 시각화합니다."""
    plt.figure(figsize=(10, 6))
    plt.bar(x_values, probabilities, width=0.4, alpha=0.7)
    plt.xticks(x_values)
    plt.xlabel('x')
    plt.ylabel('P(X = x)')
    plt.title(title)
    plt.grid(True, alpha=0.3)
    plt.show()

# 예시: 주사위 던지기의 이산확률분포
die_values = np.array([1, 2, 3, 4, 5, 6])
die_probs = np.array([1/6, 1/6, 1/6, 1/6, 1/6, 1/6])

plot_discrete_distribution(die_values, die_probs, '주사위 던지기의 확률 분포')

 

[그림1] 이산확률분포 - 주사위 던지기 확률 분포

확률질량함수(Probability Mass Function, PMF)

• 확률질량함수는 이산확률변수 $X$가 특정 값 $x$를 가질 확률을 나타내는 함수
• 확률질량함수는 이산확률분포를 표현하기 위해 사용하는 확률분포함수로 이해가능
• 예시 : 동전 2개를 동시에 던지는 시행에서 두 눈금의 합을 $X$라고 가정
  • 이때, $X$는 이산확률변수로, 확률질량함수 $f(x)$는 다음과 같이 정의 가능
  • $f(0) = P(X = 0) = \frac{1}{4}$
  • $f(1) = P(X = 1) = \frac{1}{2}$
  • $f(2) = P(X = 2) = \frac{1}{4}$
  • 확률 변수 $X$에 대한 확률질량함수라는 의미로 $f_x(x)$라고 표기하기도 한다. 

 

베르누이 시행(Bernoulli Trial)

• 오직 두 가지 결과(성공 또는 실패)만 가능한 단일 확률 시행 
• 예시 : 동전 던지기
  • 앞면(성공) 또는 뒷면(실패)이 나오는 시행
• 예시 : 품질 검사 
  • 제품이 양품(성공) 또는 불량품(실패)인지 검사하는 시행

 

베르누이 확률변수

• 베르누이 시행의 결과를 나타내는 확률 변수로, 성공(1)과 실패(0)의 두 가지 값만 가진다. 

 

베르누이 확률분포

• 베르누이 확률변수의 분포를 베르누이 확률분포라고 한다.
• 확률변수 $X$가 베르누이 분포를 따른다고 표현
• $X \sim Bern(x; p)$
  • $X$는 확률변수
  • $\sim$ 기호는 "따른다"는 의미 
  • 모수(parameter)는 세미콜론(;) 기호로 구분하여 표기한다.
  • 모수로 $p$를 가지는데, 1이 나올 확률을 의

 

베르누이 분포의 확률질량함수

• $Bern(x;p) = \begin{cases} p, & \text{if } x = 1 \\ 1 - p, & \text{if } x = 0 \end{cases}$
• 이를 간단히 표현한다면
• $Bern(x;p) = p^x (1-p)^{1-x}$
• 예시 : $p$가 0.3인 베르누이 분포

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

def plot_bernoulli_distribution(p):
    """베르누이 분포를 시각화합니다."""
    x_values = np.array([0, 1])
    probabilities = np.array([1-p, p])
    
    plt.figure(figsize=(8, 6))
    plt.bar(x_values, probabilities, width=0.4, alpha=0.7)
    plt.xticks(x_values, ['실패 (0)', '성공 (1)'])
    plt.xlabel('x')
    plt.ylabel('P(X = x)')
    plt.title(f'베르누이 분포 (p = {p})')
    plt.grid(True, alpha=0.3)
    plt.ylim(0, 1)
    plt.show()
    


# 예시: 성공 확률이 0.3인 베르누이 분포
plot_bernoulli_distribution(0.3)

[그림2] 베르누이 분포 예시 p=0.3

 

 

 

이항분포

• $N$번의 독립적인 베르누이 시행에서 성공 횟수의 확률 분포 
• 매 시행마다 성공 확률은 $p$로 동일, 각 시행은 서로 독립적(독립시행)
• 이항분포는 두 개의 매개변수로 특징지어진다. 
• 시행 횟수 $N$과 성공 확률 $p$
• 이항분포는 성공/실패 결과를 가진 반복 시행에서 성공 횟수를 모델링하는 데 사용, 여러 독립적인 베르누이 시행의 합으로 볼 수 있다. 
• 예시 : 품질 관리 
  • 100개의 제품 중 불량품 수를 모델링한다.
  • 각 제품이 불량일 확률이 $p=0.05$ 라면, 불량품 수는 이항분포 $B(100, 0.05)$를 따른다. 
• 이항 분포 확률 변수 $X$의 확률 질량 함수
  • $X \sim \text{Bin}(x; N, p) = \binom{N}{x} p^x (1-p)^{N-x}$
  • 단 $  \binom{N}{x} $는$N$개에서$x$개를 선택하는 조합의 수와 같다. 
  • $N! = N \cdot (N-1) \cdot \ldots \cdot 2 \cdot 1$

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

def plot_binomial_distribution(n, p):
    """이항분포를 시각화합니다."""
    x_values = np.arange(0, n+1)
    probabilities = stats.binom.pmf(x_values, n, p)
    
    plt.figure(figsize=(12, 6))
    plt.bar(x_values, probabilities, alpha=0.7)
    plt.xlabel('성공 횟수 (k)')
    plt.ylabel('P(X = k)')
    plt.title(f'이항분포 B({n}, {p})')
    plt.grid(True, alpha=0.3)
    plt.show()
    

# 예시: B(10, 0.3) 이항분포
plot_binomial_distribution(10, 0.3)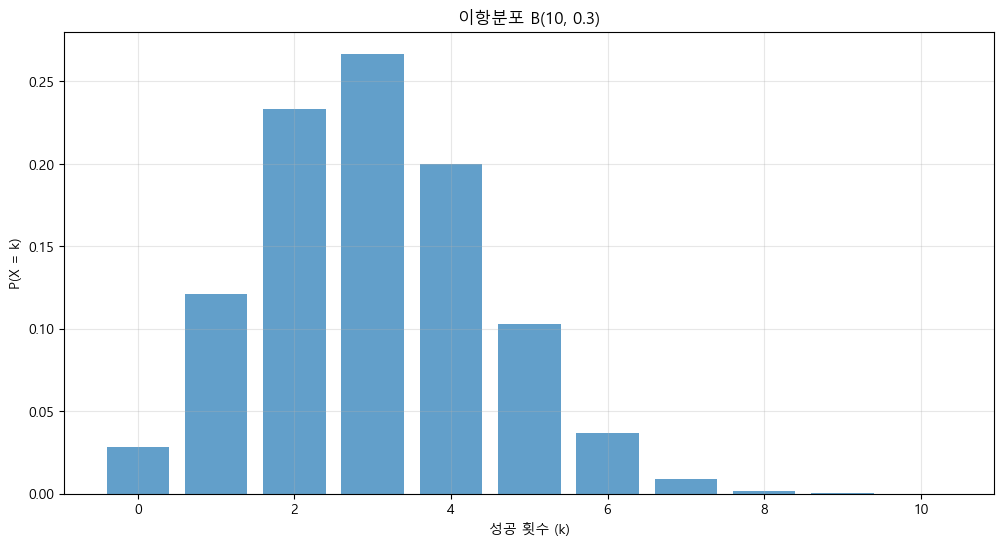

[그림3] 이항 분포 B(10, 0.3)

 

포아송 분포 

• 주어진 시간 또는 공간에서 발생 횟수에 대한 확률을 계산할 때 사용
• 단위 시간에 어떤 사건이  발생할 기댓값이  $\lambda$(람다)일 때, 그 사건이 $x$회 일어날 확률을 구할 수 있다.
• 포아송 분포의 확률 질량 함수
  • $f(x; \lambda) = \frac{e^{-\lambda} \lambda^x}{x!}$
• 포아송 분포의 평균을 $\lambda$로 표기
• $e$는 자연 상수를 의미($e$ = 2.718 ...)

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

def plot_poisson_distribution(lambda_param):
    """포아송 분포를 시각화합니다."""
    # 포아송 분포는 이론적으로 무한대까지 값을 가질 수 있지만,
    # 실질적으로는 평균 근처에 대부분의 확률이 집중됨
    max_k = int(lambda_param * 3 + 10)  # 충분히 큰 범위로 설정
    x_values = np.arange(0, max_k)
    probabilities = stats.poisson.pmf(x_values, lambda_param)
    
    plt.figure(figsize=(12, 6))
    plt.bar(x_values, probabilities, alpha=0.7)
    plt.xlabel('사건 발생 횟수 (k)')
    plt.ylabel('P(X = k)')
    plt.title(f'포아송 분포 (λ = {lambda_param})')
    plt.grid(True, alpha=0.3)
    plt.xlim(-0.5, min(max_k - 1, lambda_param * 3))  # 가독성을 위해 범위 제한
    plt.show()
    
# 예시: λ = 5인 포아송 분포
plot_poisson_distribution(5)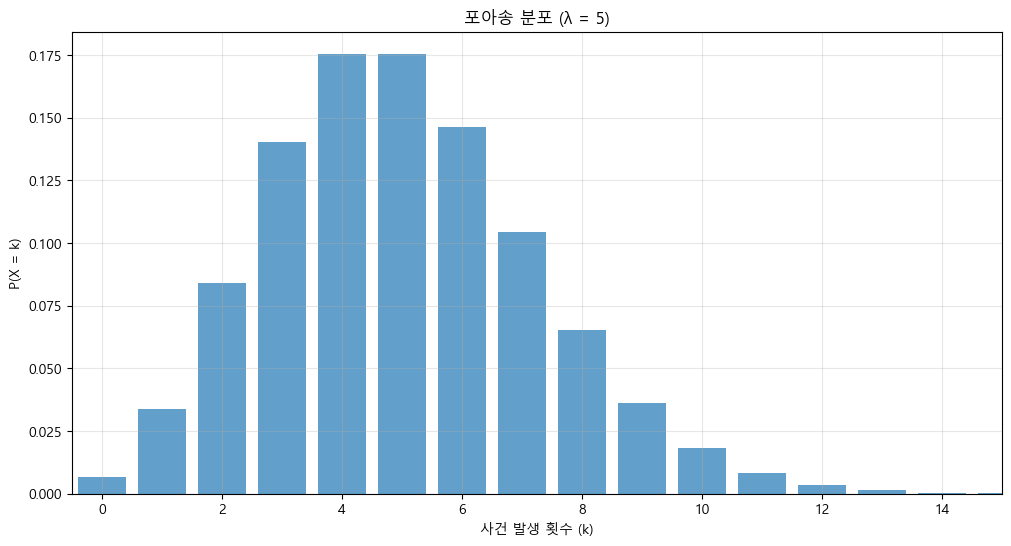

[그림4] 포아송 분포 𝜆 = 5

세 가지 분포 비교

• 베르누이 분포  : 단일 이벤트의 성공/실패를 모델링할 때 사용 (예 : 단일 제품의 양품/불량품)
• 이항분포 : 고정된 시행 횟수에서 성공의 개수를 모델링할 때 사용 (예 : 30개 제품 중 불량품의 수)
• 포아송 분포 : 시간/공간 단위당 이벤트 발생 횟수를 모델링할 때 사용 (예 : 1시간 동안 웹사이트 방문자 수)

 

AI에서의 응용

• 나이브 베이즈 분류기 :  베르누이 나이브 베이즈는 이진 특성(0/1)을 가진 데이터를 다루는 데 사용됨 (예 : 단어의 존재 여부)
• 생성 모델 : VAE, GAN과 같은 생성 모델에서 이산 데이터를 모델링할 때 사용